अध्याय–6
उत्पादन फलन तथा कुल उत्पाद, औसत उत्पाद एवं सीमांत उत्पाद की धारणाएँ
(Production Function & The Concepts of Total Product, Average Product and Marginal Product)
इस अध्याय मे हम पड़ेंगे :-
(i) उत्पादन क्या है?
(ii) उत्पादन फलन की धारणा अल्पकालीन एवं दीर्घकालीन उत्पादन फलन
(iii) उत्पादन की तीन धारणाएँ: कुल, औसत तथा सीमांत उत्पाद
(vi ) कुल, औसत तथा सीमांत उत्पाद में संबंध
उत्पादन क्या है? (What is Production ?)
प्रत्येक फर्म को वस्तुओं और सेवाओं का उत्पादन करने के लिए श्रम, भूमि, पूँजी तथा उद्यम अर्थात उत्पादन के भौतिक कारकों की आवश्यकता होती है। इसलिए यह कहा जाता है कि-
उत्पादन से अभिप्राय आगतों (Inputs ) का निर्गतों (Output) में रूपांतरण है।
(Production is the transformation of inputs into output.)
अथवा
कारकों (Factors) का वस्तुओं (Goods) में रूपांतरण है।
(Production is the transformation of factors into goods.)
अथवा
उपयोगिता के सृजन को भी उत्पादन कहा जाता है।
(Creation of utility is called production.)
उदाहरण के लिए उत्पादन के साधन( factor )/आगतों (Inputs )=
पूँजी की 10 इकाइयों तथा श्रम की 5 इकाइयों
निर्गतों (Output)/वस्तुओं (Goods)= 100 इकाइयों
अर्थात् किसी वस्तु की 100 इकाइयों का उत्पादन करने के लिए पूँजी की 10 इकाइयों तथा श्रम की 5 इकाइयों की आवश्यकता है।
उत्पादन फलन किसे कहते है ? (What is Production Function ?)
उत्पादन फलन से अभिप्राय एक वस्तु के भौतिक कारकों (श्रम, भूमि,पूँजी) तथा भौतिक उत्पादन के बीच पाए जाने वाले फलनात्मक संबंध से है।
अन्य शब्दों में उत्पादन फलन किसी फर्म के उत्पादन तथा उत्पादन के भौतिक कारकों (श्रम, भूमि,पूँजी) के बीच तकनीकी संबंध को व्यक्त करता है।
इसको निम्न प्रकार से व्यक्त किया जाता है
Q = f (L, K )
Q = वस्तु -X का भौतिक उत्पादन, f = फलन, L = श्रम की भौतिक इकाइयाँ ,K = पूँजी की भौतिक इकाइयाँ
परिभाषा ( Definition )
वाटसन के शब्दों में, “एक फर्म के भौतिक उत्पादन और उत्पादन के भौतिक कारकों के संबंध को उत्पादन फलन कहा जाता है।” [Production function is the relation between a firm’s production (output) and the material factors of production (input ). – Watson]
कौत्तसुवियानी का कहना है कि “उत्पादन फलन, कारक आगतों तथा उत्पादन के बीच संबंध स्थापित करने वाला विशुद्ध रूप से एक तकनीकी संबंध है।” (The Production function is purely a technical relation which connects factor inputs and output. -Koutsoyiannis)
उत्पादन फलन के प्रकार:-
उत्पादन फलन से पहले समय की अवधि के बारे मे जानना आवश्यक है अतः अर्थशास्त्री प्रायः समय की अवधि को दो भागों में बांटते हैं:
(1) अल्पकाल ( Short Period) :-
अल्पकाल समय की वह अवधि है जिसमें उत्पादन के सभी कारकों में परिवर्तन नहीं किया जा सकता अर्थात कुछ कारकों(जैसे भूमि,पूंजी) की मात्रा घटाई या बढ़ाई नहीं जा सकती अर्थात वे स्थिर रहती हैं।कुछ कारकों (जैसे श्रम) की मात्रा में तो परिवर्तन किया जा सकता है।इस समयावधि में उत्पादन को वर्तमान उत्पादन क्षमता तक बढ़ाया जा सकता है।
( 2 ) दीर्घकाल (Long Period)
दीर्घकाल समय की वह अवधि है जिसके दौरान सभी कारकों (जैसे श्रम,भूमि,पूंजी) की मात्रा घटाई या बढ़ाई जा सकती है। अर्थात किसी भी कारक की मात्रा स्थिर नहीं होती। इस समयावधि में उत्पादन को बाजार माँग के अनुसार घटाया-बढ़ाया जा सकता है।
समय की अवधि के आधार पर उत्पादन फलन को दो भागों में बाँटा गया है:-
(i) अल्पकालीन उत्पादन फलन (Short Run Production Function)
अल्पकाल इतनी थोड़ी अवधि है कि फर्म के लिए अपनी उत्पादन क्षमता में परिवर्तन लाना कठिन है। इसलिए केवल परिवर्तनशील कारकों (L) का अधिक प्रयोग करके ही उत्पादन को बढ़ाया जा सकता है।
उदाहरण: L (श्रम) तथा K (पूँजी) दो कारक हैं। अल्पकाल में K स्थिर (Constant ) रहता है।
40 x = f (5L, 4K )…(i)
45x = f (61, 4 K ) …(ii)
समीकरण (i) और (ii) की ओर ध्यान दें तो
हम देखते हैं कि 4 इकाइयों पर K स्थिर है। वस्तु X का 40 से 45 इकाइयों का उत्पादन L की 5 से 6 इकाइयाँ बढ़ाने के कारण ही संभव हुआ है। ऐसे उत्पादन फलन को अल्पकालीन उत्पादन फलन कहा जाता है।
इस उत्पादन फलन में, चूँकि K स्थिर है और केवल L में परिवर्तन होता है, L और K के बीच अनुपात में परिवर्तन की प्रवृत्ति पाई जाती है। इसके अनुसार, अल्पकालीन उत्पादन फलन को परिवर्ती अनुपात प्रकार का उत्पादन फलन (Variable Proportions Type Production Function) भी कहा जाता है।
(ii) दीर्घकालीन उत्पादन फलन (Long Run Production Function )
दीर्घकाल समय की वह अवधि है जिसमें सभी कारक(श्रम,भूमि,पूंजी) परिवर्तनशील हैं। इसलिए, उत्पादन के सभी कारकों का अधिक प्रयोग करके उत्पादन को बढ़ाया जा सकता है। दीर्घकाल में K भी परिवर्तनशील है जो अल्पकाल में स्थिर (Constant ) रहता है।
समीकरण (iii) तथा (iv) को ध्यान में लाएँ:-
40 x = f (5L,4 K)…..(iii)
80x = f (10 L,8K) …..(iv)
इसका अर्थ यह है कि जब सभी कारक आगतों (L और K) को दुगना किया जाता है तब उत्पादन भी दुगना हो जाता है। ऐसा उत्पादन फलन दीर्घकालीन उत्पादन फलन कहलाता है। इसे समान अनुपात प्रकार का उत्पादन फलन (Constant Proportions Type Production Function) भी कहा जाता है।
Diagrammatic Illustration:-
चित्र 1(A) तथा चित्र 1(B) क्रमश: समान अनुपात प्रकार के उत्पादन फलन तथा परिवर्ती अनुपात प्रकार के उत्पादन फलन के अंतर को व्यक्त कर रहे हैं।
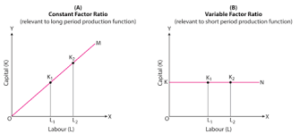
चित्र (A) में एक सरल रेखा मूल बिंदु से शुरू होती है, जिसमें श्रम तथा पूँजी के समान अनुपात का उत्पादन के विभिन्न स्तरों के लिए प्रयोग किया गया है। OX अक्ष पर श्रम को और OY अक्ष पर पूँजी को दिखाया गया है।
चित्र (B) में OX के समांतर सीधी रेखा OY – अक्ष से शुरू होती है जो यह प्रकट करती है कि पूँजी की OK इकाइयाँ स्थिर हैं और उत्पादन के ऊँचे स्तर को तभी प्राप्त किया जा सकता है, जब श्रम के आगत (Input) या कारक की मात्रा OL1 से बढ़ाकर OL2 कर दी जाती है।
इसका अर्थ यह है कि उत्पादन के स्तर में परिवर्तन होने से कारक अनुपात में परिवर्तन होने की प्रवृत्ति पाई जाती है।
समान या स्थिर अनुपात तथा परिवर्ती अनुपात प्रकार के उत्पादन फलन के बीच के अंतर स्पष्ट करें :-
| दीर्घकालीन (समान या स्थिर अनुपात) उत्पादन फलन | अल्पकालीन (परिवर्ती अनुपात ) उत्पादन फलन |
| 1. दीर्घकालीन में कारक अनुपात समान रहता है चाहे उत्पादन का स्तर कुछ भी क्यों न हो। | अल्पकालीन उत्पादन फलन में उत्पादन के स्तर में परिवर्तन होने के साथ कारक अनुपात में परिवर्तन होता है। |
| 2. सभी कारकों (श्रम,भूमि,पूंजी) के प्रयोग की मात्रा को बढ़ाकर उत्पादन को बढाया जा सकता है। | 2. कुछ परिवर्ती कारकों(जैसे श्रम) के प्रयोग में वृद्धि करके ही उत्पादन को बढाया जा सकता है। |
| 3. उत्पादन के स्तर में परिवर्तन के साथ उत्पादन के पैमाने (या उत्पादन क्षमता या प्लॉट के आकार ) में परिवर्तन होने की प्रवृत्ति पाई जाती है। | 3. उत्पादन के स्तर में परिवर्तन होने से उत्पादन के पैमाने में परिवर्तन नहीं होता। |
| 40 x = f (5L, 4K )…(i)
45x = f (6L, 4 K ) …(ii) |
40 x = f (5L,4 K)…..(iii)
80x = f (10L,8K) …..(iv) |
उत्पादन की तीन धारणाएँ: कुल, औसत तथा सीमांत उत्पाद
Three Concepts of Production-Total, Average and Marginal Product
(1) कुल उत्पाद (Total Product-TP)
(2) सीमांत उत्पाद (Marginal Product – MP )
(3) औसत उत्पाद (Average Product-AP)
कुल उत्पाद (Total Product ) :-
एक निश्चित समय में उत्पादित की गई वस्तुओं तथा सेवाओं की कुल मात्रा को कुल उत्पाद कहा जाता है । (Total product is the total amount of goods and services produced in a given period.)
मान लीजिए एक किसान भूमि के निश्चित टुकड़े अर्थात् 1 हेक्टेयर पर श्रम की एक इकाई का प्रयोग करके 2 क्विंटल गेहूँ का उत्पादन करता है तो 2 क्विंटल गेहूँ को एक श्रमिक का कुल उत्पाद कहा जाएगा। इस उदाहरण में भूमि उत्पादन का स्थिर कारक है तथा श्रम परिवर्तनशील कारक है। गेहूँ के उत्पादन को बढ़ाने के लिए हम जैसे-जैसे परिवर्तनशील कारक की अधिक इकाइयों का प्रयोग करते हैं तो आरंभ में कुल उत्पाद अधिक तेजी से बढ़ता है। इसके पश्चात कुल उत्पाद धीमी गति से बढ़ता है और एक बिंदु ऐसा आ जाता है जहाँ कुल उत्पाद बढ़ने के स्थान पर कम होने लगता है। इसका कारण यह है कि आरंभ में परिवर्तनशील कारक की कम इकाई लगाये जाने के कारण स्थिर कारक का पूर्ण उपयोग नहीं हो पाता। परंतु जैसे-जैसे हम परिवर्तनशील कारक की अधिक इकाइयों का प्रयोग करते जाते हैं, स्थिर कारकों का अधिक कुशलतापूर्वक उपयोग होता जाता है। परंतु एक सीमा के पश्चात परिवर्तनशील कारक की अधिक मात्रा का उपयोग करने से उत्पादन गिरने लगता है क्योंकि फैक्ट्री में अधिक भीड़-भाड़ हो जाती है या भूमि पर अधिक श्रमिक काम करने लगते हैं जिससे श्रमिकों की कुशलता बढ़ने के स्थान पर कम होने लगती है।
तालिका द्वारा कुल उत्पाद की धारणा को स्पष्ट किया जा सकता है। यह तालिका इस मान्यता पर बनाई गई है कि भूमि उत्पादन का स्थिर कारक है तथा श्रम परिवर्तनशील कारक हैं।
Table-Total Production
| भूमि की इकाइयाँ(हेक्टेयर) | श्रम की इकाइयाँ | कुल उत्पाद (क्विंटल) |
| 1 | 1 | 2 |
| 1 | 2 | 5 |
| 1 | 3 | 9 |
| 1 | 4 | 11 |
| 1 | 5 | 12 |
| 1 | 6 | 12 |
| 1 | 7 | 11 |
तालिका से ज्ञात होता है कि जब श्रम की 6 इकाइयों का प्रयोग किया जा रहा है तो कुल उत्पाद अधिकतम है। इसके पश्चात कुल उत्पाद कम हो गया है।
सीमांत उत्पाद (Marginal Product):-
परिवर्तनशील कारक की एक इकाई का कम या अधिक प्रयोग करने से कुल उत्पाद में जो अंतर आता है उसे सीमांत उत्पाद कहा जाता है |(Marginal production is the change in total product due to application of one more or less unit of variable factor.)
उदाहरण के लिए, यदि श्रम की 1 इकाई लगाने से 2 क्विंटल अनाज का उत्पादन होता है तथा 2 इकाई लगाने से 5 क्विंटल अनाज का उत्पादन होता है तो दूसरी इकाई का सीमांत उत्पाद (5 – 2) = 3 क्विंटल होगा । सीमांत उत्पाद की जानकारी निम्नलिखित सूत्र की सहायता से प्राप्त की जा सकती है:
MPn = TPn – TPn -1
अथवा
ΔΤΡ
MP = —————
ΔL
(यहाँ, MPn = n इकाई का सीमांत उत्पाद; TPn=n इकाई का कुल उत्पाद; TPn−1 = n -1 इकाई का कुल उत्पाद, ΔΤΡ = कुल उत्पाद में परिवर्तन; ΔL = श्रम अर्थात् परिवर्तनशील कारक की मात्रा में परिवर्तन ।)
सीमांत उत्पाद की धारणा को निम्नलिखित तालिका 2 द्वारा स्पष्ट किया जा सकता है।
तालिका -सीमांत उत्पाद (Marginal Product )
| भूमि की इकाइयाँ (हेक्टेयर) | श्रम की इकाइयाँ | कुल उत्पाद (क्विंटल) | सीमांत उत्पाद |
| 0 | 0 | 0 | – |
| 1 | 1 | 2 | 2-0=2 |
| 1 | 2 | 5 | 5-2=3 |
| 1 | 3 | 9 | 9-5=4 |
| 1 | 4 | 11 | 11-9=2 |
| 1 | 5 | 12 | 12–11=1 |
| 1 | 6 | 12 | 12-12=0 |
| 1 | 7 | 11 | 11-12=-1 |
तालिका से ज्ञात होता है कि आरंभ में सीमांत उत्पाद बढ़ता गया है। इसके पश्चात सीमांत उत्पाद कम हो गया है परंतु धनात्मक (Positive) है। श्रम की छठी इकाई पर सीमांत उत्पाद शून्य(Zero)हो गया है। इसके पश्चात सीमांत उत्पाद ऋणात्मक (Negative) हो गया है।
औसत उत्पाद (Average Product):–
परिवर्तनशील कारक की प्रति इकाई उत्पादन को औसत उत्पाद कहा जाता है। (Average product is per unit production of the variable factor.)
कुल उत्पाद को परिवर्तनशील कारक की कुल इकाइयों से भाग देने पर औसत उत्पाद ज्ञात किया जा सकता है । औसत उत्पाद का अनुमान निम्नलिखित सूत्र से लगाया जा सकता है: –
TP
AP = ———-
L
(यहाँ, AP = औसत उत्पाद; TP = कुल उत्पाद; L = श्रम अर्थात परिवर्तनशील कारक की इकाइयाँ।)
उदाहरण के लिए, यदि 4 श्रमिकों का कुल उत्पाद 12 क्विंटल है तो इनका औसत उत्पाद = 3 औसत उत्पाद
औसत उत्पाद की धारणा को तालिका 3 की सहायता से स्पष्ट किया जा सकता है।
Table-2-Avrage Prodution
| भूमि की इकाइयाँ(हेक्टेयर) | श्रम की इकाइयाँ | कुल उत्पाद (क्विंटल) | औसत उत्पाद |
| 1 | 1 | 2 | 2÷1=2 |
| 1 | 2 | 5 | 5÷2=2.5 |
| 1 | 3 | 9 | 9÷3=3 |
| 1 | 4 | 11 | 11÷4=2.7 |
| 1 | 5 | 12 | 12 ÷ 5 = 2.4 |
| 1 | 6 | 12 | 12÷6=2 |
| 1 | 7 | 11 | 11÷ 7 = 1.5 |
तालिका से ज्ञात होता है कि आरंभ में श्रम की 3 इकाइयाँ तक औसत उत्पाद बढ़ रहा है। तीसरी इकाई के बाद ये कम होना आरंभ हो गया है। परंतु औसत उत्पाद सदैव धनात्मक (Positive) रहता है। यह सीमांत उत्पाद की तरह शून्य (Zero) या ऋणात्मक (Negative) नहीं होता
एक उपयुक्त रेखाचित्र और तालिका का प्रयोग करते हुए कुल उत्पाद,सीमांत उत्पाद तथा और औसत उत्पाद के बीच संबंध की व्याख्या करें। (Relation between MP and TP)
तालिका 2 तथा चित्र 2 यह स्पष्ट करते हैं कि TP, MP और AP एक-दूसरे से किस प्रकार संबंधित हैं।
तालिका – कुल उत्पाद, औसत उत्पाद तथा सीमांत उत्पाद (TP, AP and MP)
| भूमि (हेक्टेयर) – स्थिर कारक | परिवर्ती कारक ( Labour) | सीमांत उत्पाद (MP) | कुल उत्पाद
(TP= ΣMP) |
औसत उत्पाद AP = TP/L |
| 1 | 0 | – | 0 | – |
| 1 | 1 | 6 | 6 | 6 |
| 1 | 2 | 14 | 20 | 10 |
| 1 | 3 | 28 | 48 | 16 |
| 1 | 4 | 24 | 72 | 18 |
| 1 | 5 | 8 | 80 | 16 |
| 1 | 6 | 4 | 84 | 14 |
| 1 | 7 | 0 | 84 | 12 |
| 1 | 8 | -4 | 80 | 10 |
तालिका यह स्पष्ट करते हैं कि TP तथा MP एक-दूसरे से किस प्रकार संबंधित हैं।
(i) जब तक सीमांत उत्पाद (MP) बढ़ता :-
जब तक सीमांत उत्पाद (MP) बढ़ रहा होता है, कुल उत्पाद (TP) भी बढ़ती दर पर बढ़ रहा होता है। तालिका से प्रकट होता है कि परिवर्ती कारक की तीसरी इकाई तक चावल का सीमांत उत्पाद (MP) 6 से 14 से 28 टन बढ़ रहा है। इसके अनुसार कुल उत्पाद में श्रम की पहली इकाई का योगदान 6 टन चावल, दूसरी इकाई का योगदान 14 टन और तीसरी इकाई का योगदान 28 टन है। इसका अर्थ यह है कुल उत्पाद (TP) बढ़ती दर पर बढ़ रहा है।
(ii) जब सीमांत उत्पाद (MP) घटता :-
जब सीमांत उत्पाद (MP) घटना शुरू हो जाता है, कुल उत्पाद (TP) केवल ह्रासमान (घटती) दर पर बढ़ता है । यह तब हुआ है जब श्रम की चौथी इकाई का प्रयोग किया गया है। श्रम की चौथी इकाई का सीमांत उत्पाद (MP) 24 टन चावल, पाँचवीं का 8 टन चावल और छठी का केवल 4 टन चावल है। इसके अनुसार, श्रम की जब चौथी इकाई का प्रयोग किया गया है तब कुल उत्पाद (TP) में 24 टन की वृद्धि हुई है, श्रम की जब पाँचवी इकाई का प्रयोग किया गया है तब है कुल उत्पाद में 8 टन की वृद्धि हुई है और जब छठी इकाई का प्रयोग किया गया है, तब कुल उत्पाद में केवल 4 टन की वृद्धि हुई है। इसका अर्थ यह है कि कुल उत्पाद में केवल ह्रासमान (घटती) दर पर वृद्धि हो रही है।
iii) जब सीमांत उत्पाद शून्य (MP = 0) होता है
जब सीमांत उत्पाद शून्य (MP = 0) है, तब कुल उत्पाद में कोई वृद्धि नहीं होती है। ऐसा तब होता है जब सातवीं इकाई का प्रयोग किया जाता है। सीमांत उत्पाद (MP) के शून्य होने पर, कुल उत्पाद (TP) अधिकतम है।
(iv) जब MP ऋणात्मक होता है :-
(iv) जब MP ऋणात्मक है, TP गिरना शुरू हो जाता है। यह तब होता है जब श्रम की 8वीं इकाई काम पर लगाई जाती है। कुल उत्पाद (TP) 84 से कम हो कर 80 हो जाता है और तब MP = 80 – 84 = – 4 है।
सीमांत उत्पाद कुल उत्पाद की दर है (MP is the Rate of TP)
बढ़ते सीमांत उत्पाद का अर्थ है कुल उत्पाद का बढ़ती दर पर बढ़ना ।
ह्रासमान सीमांत उत्पाद का अर्थ है कि कुल उत्पाद ह्रासमान (घटती) दर पर बढ़ रहा है।
शून्य सीमांत उत्पाद का अर्थ है कि कुल उत्पाद का बढ़ना रुक जाता है
ऋणात्मक MP का अर्थ है TP में गिरावट |
चित्र 2 यह स्पष्ट करते हैं कि TP और MP एक-दूसरे से किस प्रकार संबंधित हैं।
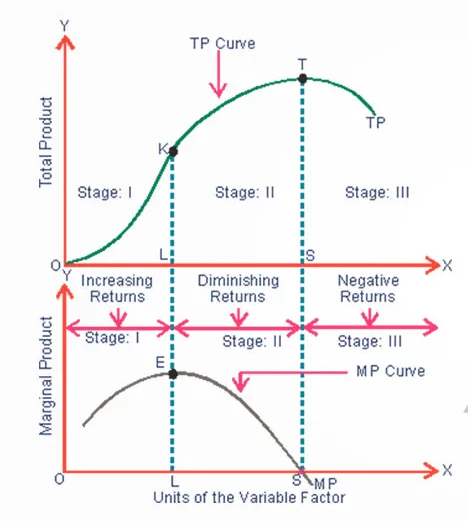
औसत उत्पाद तथा सीमांत उत्पाद के बीच संबंध (Observations: Relation between AP and MP)
औसत उत्पाद (AP) तथा सीमांत उत्पाद (MP) के बीच निम्नलिखित संबंध पाया जाता है:-
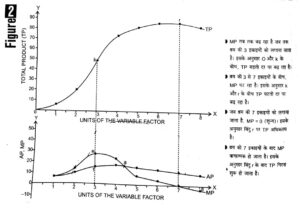
(i) औसत उत्पाद (AP) तथा सीमांत उत्पाद (MP) दोनों का अनुमान कुल उत्पाद (TP) की सहायता से लगाया जाता है।
AP = TP ÷ N , MP = TPn – TPn-1
(ii) जब औसत उत्पाद बढ़ता है तो सीमांत उत्पाद भी बढ़ता है किंतु सीमांत उत्पाद औसत उत्पाद से अधिक तेजी से बढ़ता है
(MP > AP)। चित्र 2 में ऐसा बिंदु ‘a’ से पहले तक है जब औसत उत्पाद अपने उच्चतम बिंदु पर है।
(iii) जब औसत उत्पाद घटता है तो सीमांत उत्पाद भी घटता है किंतु सीमांत उत्पाद औसत उत्पाद से अधिक तेजी से घटता है
(MP < AP)। चित्र 2 में ऐसा बिंदु ‘a’ के बाद होता है जहाँ औसत उत्पाद अपनी चोटी या ऊपरी सिरे पर है।
(iv) जब औसत उत्पाद अधिकतम तथा स्थिर होता है तो सीमांत उत्पाद औसत उत्पाद के बराबर होता है अर्थात MP = AP चित्र 2 में यह ठीक बिंदु ‘a’ पर है।
(v) औसत उत्पाद सदैव धनात्मक रहता है परंतु सीमांत उत्पाद धनात्मक, शून्य या ऋणात्मक कुछ भी हो सकता है।